Accueil > Electronique > FPGA > Filtre numérique du 1er ordre
En cours de rédaction
Filtre numérique du 1er ordre
samedi 19 juin 2010, par
Introduction
La description qui suit permet de filtrer des échantillons en temps réel. Le filtre est implémenté sous sa forme dit directe.
La synthèse du filtre (transformée bilinéaire)
Commençons par un peu de théorie afin de transformer un filtre continu vers un filtre discret.
La forme générale du filtre dans le domaine de Laplace est :
![]()
En substituant ![]() par
par ![]() dans
dans ![]() , on obtient :
, on obtient :
![]()
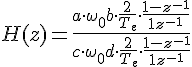
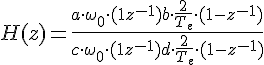
On obtient :
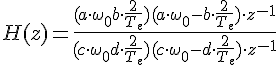
Posons ![]() :
:
![]()
![]()
On obtient l’équation aux différences :
![s[k] = e[k] \cdot \frac{a \cdot \omega_{0} + b \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}} + e[k-1] \cdot \frac{a \cdot \omega_{0} - b \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}} - s[k-1] \cdot \frac{c \cdot \omega_{0} - d \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}} s[k] = e[k] \cdot \frac{a \cdot \omega_{0} + b \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}} + e[k-1] \cdot \frac{a \cdot \omega_{0} - b \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}} - s[k-1] \cdot \frac{c \cdot \omega_{0} - d \cdot \frac{2}{T_{e}}}{c \cdot \omega_{0} + d \cdot \frac{2}{T_{e}}}](local/cache-vignettes/L480xH65/3e545dbbf704593893832c4e7dfbf937-93c14.png?1587815855)
Et finalement, l’équation aux différences qui sera implémentée dans la description VHDL :
![]()
La description
L’implémentation se base sur trois multiplieur série et un additionneur série.
La description se décompose en quatre parties :
![]() le multiplieur série,
le multiplieur série,
![]() l’additionneur série,
l’additionneur série,
![]() le registre à décalage de sortie et
le registre à décalage de sortie et
![]() le séquenceur.
le séquenceur.
Le multiplieur série
Le multiplieur est sous une forme séquencée qui nécessite 37 coups d’horloge afin de produire le résultat. Le signal ’start’ démarre le processus de multiplication. Le bus ’selector’ provient d’un compteur (qui est mutualisé par plusieurs instances du multiplieur) et fournit un auxiliaire dans l’opération de multiplication. ’a’ et ’b’ sont respectivement le multiplicande et le multiplicateur. Le produit se présente sous la forme d’un flux série, idéal pour alimenter un additionneur série.
L’additionneur série
L’additionneur série présenté ici est basé sur un additionneur complet avec une rétroaction des retenues. Il additionne trois termes correspondant aux produits des multiplieurs décrits ci-dessus. La somme se présente sous un flux série.